没听课的我要写自定义三阶贝塞尔曲线……瞎写了一个点,突然有了点思路,然后写了好一阵,写完了决定md一下思路,嗯,也用不到,老师说放到github上点点star,我想想还是算了,太菜
进入正题
自定义三阶贝塞尔曲线首先是 需要用canvas去画的,并且你每拖动一个点,都要重绘一次。所以一开始我直接用bezierCurveTo画了一个三阶曲线,妄想去让他变弯……事实证明不行。
所以参考了一下一个自定义贝塞尔曲线动画的网站,他会给顶点和关键点做成一个可拖拽的圆,然后通过改变圆的位置改变贝塞尔曲线的关键点,搜噶!
首先肯定要有个canvas,并且在js中获取它。
1
| <canvas id="canvas" width="800" height="500"></canvas>
|
1
2
| var canvas = document.getElementById('canvas');
var context = canvas.getContext('2d');
|
因为要拖动四个点来改变三阶贝塞尔曲线的值,所以我把所有的点放到一个point对象里,然后在初始化的函数init()中定义
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
function init(quadratic) {
point = {
p1: {
x: 100,
y: 250
},
p2: {
x: 400,
y: 250
}
}
point.cp1 = {
x: 150,
y: 100
},
point.cp2 = {
x: 350,
y: 100
},
style = {
line: {
width: 6,
color: 'red'
},
cpline: {
width: 2,
color: '#777'
},
point: {
radius: 10,
width: 2,
color: 'rgb(55, 255, 55)',
fill: 'rgba(102, 217, 255 , 0.7)',
arc1: 0,
arc2: Math.PI * 2
}
}
canvas.onmousedown = dragStart;
canvas.onmousemove = dragging;
canvas.onmouseup = dragEnd;
DrawCanvas();
}
|
然后要画出曲线、左边点以及右边点的连线(为了好看),要注意因为每次都是重绘所以要把画布清空
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| function DrawCanvas() {
context.clearRect(0, 0, canvas.width, canvas.height);
context.lineWidth = style.cpline.width;
context.strokeStyle = style.cpline.color;
context.beginPath();
context.moveTo(point.p1.x, point.p1.y);
context.lineTo(point.cp1.x, point.cp1.y);
context.moveTo(point.p2.x, point.p2.y);
context.lineTo(point.cp2.x, point.cp2.y);
context.stroke();
context.lineWidth = style.line.width;
context.strokeStyle = style.line.color;
context.beginPath();
context.moveTo(point.p1.x, point.p1.y);
context.bezierCurveTo(point.cp1.x, point.cp1.y, point.cp2.x, point.cp2.y, point.p2.x, point.p2.y);
context.stroke();
for (const p in point) {
context.lineWidth = style.point.width;
context.strokeStyle = style.point.color;
context.fillStyle = style.point.fill;
context.beginPath();
context.arc(point[p].x, point[p].y, style.point.radius, style.point.arc1, style.point.arc2)
context.fill();
context.stroke();
}
}
|
画也画完了,我构思的时候卡住的门槛就来了……怎么判断鼠标是不是点在了那四个圆里呢,想啥呢百度就完事了,然后发现了一个什么判断是不是在当前路径的东西,嗯???什么玩意不会用,所以就另辟蹊径,判断鼠标点击位置在不在圆里,高中数学?初中数学?点到圆心的距离小于半径,嗯我真聪明
想好了就开始写吧
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| function dragStart(e) {
e = MousePos(e);
console.log(e);
var dx,
dy;
for (var p in point) {
dx = point[p].x - e.x;
dy = point[p].y - e.y;
if ((dx * dx) + (dy * dy) < style.point.radius * style.point.radius) {
console.log(1);
drag = p;
dPoint = e;
return;
}
}
}
function dragging(e) {
if (drag) {
e = MousePos(e);
point[drag].x += e.x - dPoint.x;
point[drag].y += e.y - dPoint.y;
dPoint = e;
DrawCanvas();
}
}
function dragEnd(e) {
drag = null;
DrawCanvas();
}
|
ps:把鼠标相对于画布的位置封装了一下
1
2
3
4
5
6
7
8
9
|
function MousePos(e) {
e = e ? e : window.event;
return {
x: e.pageX - canvas.offsetLeft,
y: e.pageY - canvas.offsetTop
}
}
|
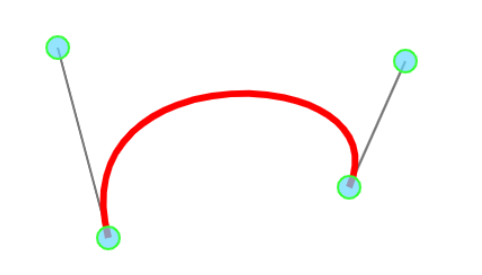
然后一个自定义贝塞尔曲线就完成了,其实还好,就是有点……没听课!
